LeetCode-第438场周赛

本文最后更新于：2025年2月23日 晚上

LeetCode-第438场周赛

第一次参加LeetCode周赛，只完成了前两题。第三题一直超时

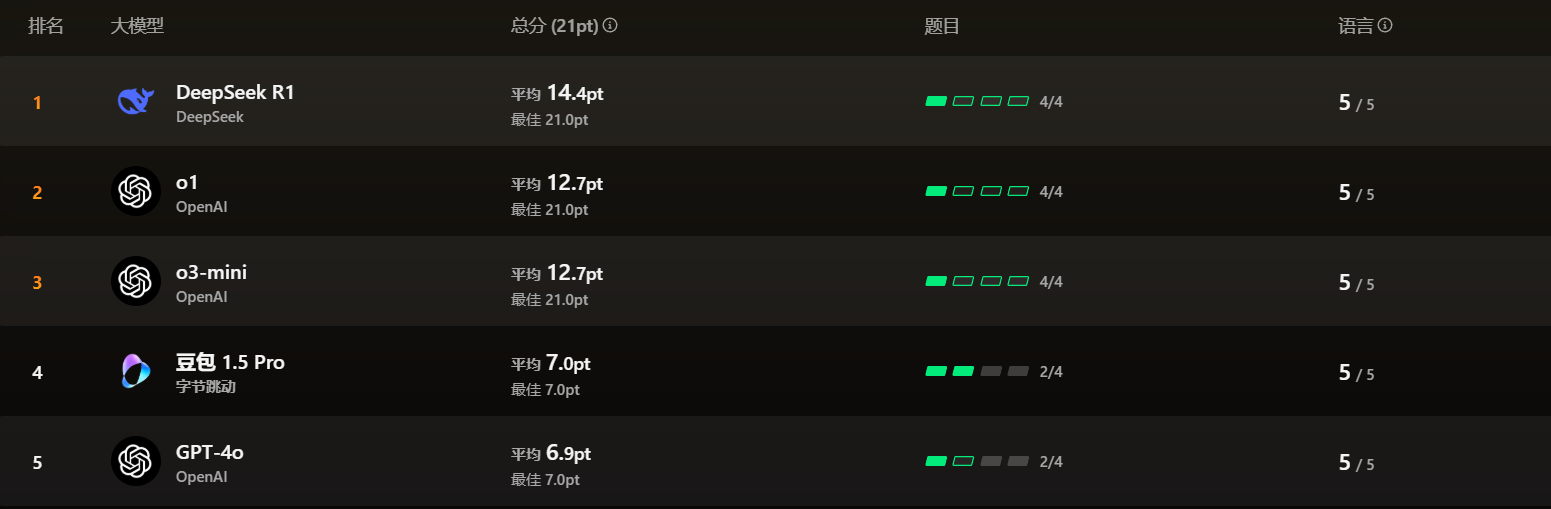
排名 868/2401 豆包1.5 Pro水平

image-20250223124127089

Q1. 判断操作后字符串中的数字是否相等Ⅰ

题目描述

给你一个由数字组成的字符串 s 。重复执行以下操作，直到字符串恰好包含 两个 数字：

  • 从第一个数字开始，对于 s 中的每一对连续数字，计算这两个数字的和 模 10。
  • 用计算得到的新数字依次替换 s 的每一个字符，并保持原本的顺序。
    如果 s 最后剩下的两个数字 相同 ，返回 true 。否则，返回 false。

示例 1：

输入： s = “3902”

输出： true

解释：

一开始，s = “3902”
第一次操作：
(s[0] + s[1]) % 10 = (3 + 9) % 10 = 2
(s[1] + s[2]) % 10 = (9 + 0) % 10 = 9
(s[2] + s[3]) % 10 = (0 + 2) % 10 = 2
s 变为 “292”
第二次操作：
(s[0] + s[1]) % 10 = (2 + 9) % 10 = 1
(s[1] + s[2]) % 10 = (9 + 2) % 10 = 1
s 变为 “11”
由于 “11” 中的数字相同，输出为 true。

示例 2：

输入： s = “34789”

输出： false

解释：

一开始，s = “34789”。
第一次操作后，s = “7157”。
第二次操作后，s = “862”。
第三次操作后，s = “48”。
由于 ‘4’ != ‘8’，输出为 false。

提示：

  • 3 <= s.length <= 100
  • s 仅由数字组成。

题解

数据范围小，模拟即可

1
2
3
4
5
6
7
8
class Solution:
    def hasSameDigits(self, s: str) -> bool:
        while len(s) != 2:
            temp = []
            for i in range(len(s) - 1):
                temp.append((int(s[i]) + int(s[i+1])) % 10)
            s = temp
        return s[0] == s[1]

Q2. 提取至多K个元素的总和

给你一个大小为 n x m 的二维矩阵 grid ，以及一个长度为 n 的整数数组 limits ，和一个整数 k 。你的目标是从矩阵 grid 中提取出 至多 k 个元素，并计算这些元素的最大总和，提取时需满足以下限制：

  • 从 grid 的第 i 行提取的元素数量不超过 limits[i] 。

返回最大总和。

示例 1：

输入：grid = [[1,2],[3,4]], limits = [1,2], k = 2

输出：7

解释：

从第 2 行提取至多 2 个元素，取出 4 和 3 。
至多提取 2 个元素时的最大总和 4 + 3 = 7 。

示例 2：

输入：grid = [[5,3,7],[8,2,6]], limits = [2,2], k = 3

输出：21

解释：

从第 1 行提取至多 2 个元素，取出 7 。
从第 2 行提取至多 2 个元素，取出 8 和 6 。
至多提取 3 个元素时的最大总和 7 + 8 + 6 = 21 。

提示：

  • n == grid.length == limits.length
  • m == grid[i].length
  • 1 <= n, m <= 500
  • 0 <= grid[i][j] <= 10^5
  • 0 <= limits[i] <= m
  • 0 <= k <= min(n * m, sum(limits))

题解

排序

1
2
3
4
5
6
7
8
9
10
class Solution:
    def maxSum(self, grid: List[List[int]], limits: List[int], k: int) -> int:
        n, m = len(grid), len(grid[0])
        temp = []
        for i in range(n):
            grid[i].sort(reverse = True)
            for j in range(limits[i]):
                temp.append(grid[i][j])
        temp.sort(reverse = True)
        return sum(temp[:k])

Q3. 判断操作后字符串中的数字是否相等Ⅱ

题目与Q1一致，但数据范围更大

3 <= s.length <= 10^5

解法一-组合数求解

1
2
3
4
5
6
长度 系数
2	1
3	1 1
4	1 2 1
5	1 3 3 1
6	1 4 6 4 1
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def hasSameDigits(self, s: str) -> bool:
        def combination(n, k):
            return math.comb(n, k)
        sum_0, sum_1 = 0, 0
        n = len(s)
        for i in range(n - 1):
            sum_0 += int(s[i]) * combination(n-2, i)
            sum_0 %= 10
        for i in range(1, n):
            sum_1 += int(s[i]) * combination(n-2, i-1)
            sum_1 %= 10
        return sum_0 == sum_1

超出时间限制，优化组合数阶乘求解和两次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def hasSameDigits(self, s: str) -> bool:
        n = len(s)
        sum_0, sum_1 = 0, 0      
        # 初始化组合数 C(n-2, 0) = 1
        comb_0 = 1
        
        for i in range(n - 1):
            sum_0 += int(s[i]) * comb_0
            sum_0 %= 10
            
            sum_1 += int(s[i + 1]) * comb_0
            sum_1 %= 10
            
            if i < n - 2:
                comb_0 = comb_0 * (n - 2 - i) // (i + 1)
        
        return sum_0 == sum_1

还是超出了时间限制

全服第一解法

看不懂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution:
    def hasSameDigits(self, s: str) -> bool:
        n = len(s)
        if n == 2:
            return (s[0] == s[1])
        
        digits = list(map(int, s))
        N = n - 2
    
        binom_mod5 = [[0]*5 for _ in range(5)]
        for i in range(5):
            binom_mod5[i][0] = 1
            for j in range(1, i+1):
                from math import comb
                binom_mod5[i][j] = comb(i, j) % 5
        
        combine_map = {}
        for x in range(10):
            pair = (x % 2, x % 5)
            combine_map[pair] = x
        
        def binom_mod2(n, k):
            return 1 if (k & ~n) == 0 else 0
        
        def binom_mod5_func(n, k):
            res = 1
            while n > 0 or k > 0:
                n5 = n % 5
                k5 = k % 5
                if k5 > n5:
                    return 0
                res = (res * binom_mod5[n5][k5]) % 5
                n //= 5
                k //= 5
            return res
        
        def binom_mod10(n, k):
            b2 = binom_mod2(n, k)
            b5 = binom_mod5_func(n, k)
            return combine_map[(b2, b5)]
        
        binom_table = [0]*(N+1)
        for k in range(N+1):
            binom_table[k] = binom_mod10(N, k)
        d0 = 0
        d1 = 0
        for m in range(N+1):
            c = binom_table[m]
            d0 = (d0 + digits[m]*c) % 10
            d1 = (d1 + digits[m+1]*c) % 10    
        return (d0 == d1)

1. 计算组合数模 5 和模 2

在这个实现中，组合数的计算被分成了两部分：模 2 和模 5。组合数模 10 可以通过结合模 2 和模 5 的结果来求得，类似于中国剩余定理的思路。具体地：

  • 模 2：通过位操作来判断组合数的结果，binom_mod2 函数判断$C(n, k) \mod 2$ 的结果。这是因为对于二项式系数 $C(n, k)$，模 2 的结果仅仅由二进制表示中的某些特定规则决定。
  • 模 5：计算组合数的模 5，通过预处理的 binom_mod5 表来加速组合数的计算。这里使用了递推和分解的方法，避免了直接计算阶乘。

2. 组合数模 10 的计算

为了计算组合数的模 10，代码通过结合 binom_mod2 和 binom_mod5_func 的结果，并使用 combine_map 来映射组合数的模 2 和模 5 的值到模 10 的值。

  • binom_mod2 用于计算组合数模 2。
  • binom_mod5_func 用于计算组合数模 5。通过递推和取模的方法，避免了直接计算大数阶乘。

之后，通过 combine_map，将 (mod 2, mod 5) 对应的组合数模 10 的结果提取出来。

3. 优化和预处理

  • 预处理组合数：代码在开始时就预处理了组合数的模 5，保存在 binom_mod5 表中。这样，在后续计算中就可以直接使用这些预计算的值，而不需要每次都重新计算组合数。
  • 逐步计算：每轮计算组合数时，通过递推公式，逐步计算并更新组合数模 10 的结果。通过这样的方法，避免了重复计算，显著提高了效率。

4. 优化的关键步骤

  • 合并模 2 和模 5 的结果：通过 combine_map 映射模 2 和模 5 的组合结果到模 10。由于模 2 和模 5 对组合数的影响各自独立，这个方法巧妙地将两者的结果结合起来。
  • 递推而不是阶乘计算：通过递推计算组合数的模 5，避免了直接计算阶乘，这对于大规模数据尤其有效。
  • 位操作判断组合数模 2：通过位操作实现 $C(n, k) \mod 2$的计算，这在处理二项式系数时非常高效。

5. 算法分析

  • 时间复杂度：该算法的时间复杂度主要由两部分组成：

    1. 预处理阶段：计算组合数模 5，时间复杂度为 O(n)，其中 n 是输入字符串的长度。
  1. 计算阶段：遍历字符串并计算组合数的结果，时间复杂度为 O(n)，因为每次更新的计算量是常数时间。

Q4. 正方形上的点之间的最大距离

题目描述

给你一个整数 side，表示一个正方形的边长，正方形的四个角分别位于笛卡尔平面的 (0, 0) ，(0, side) ，(side, 0) 和 (side, side) 处。

同时给你一个 正整数 k 和一个二维整数数组 points，其中 points[i] = [xi, yi]表示一个点在正方形边界上的坐标。

你需要从 points 中选择 k 个元素，使得任意两个点之间的 最小 曼哈顿距离 最大化 。

返回选定的 k 个点之间的 最小 曼哈顿距离的 最大 可能值。

两个点 (xi, yi) 和 (xj, yj) 之间的曼哈顿距离为 |xi - xj| + |yi - yj|。

示例 1：

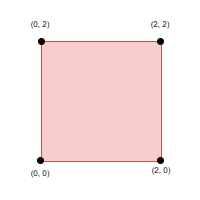
输入： side = 2, points = [[0,2],[2,0],[2,2],[0,0]], k = 4

输出： 2

解释：

选择所有四个点。

示例 2：

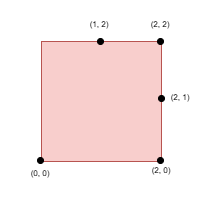
输入： side = 2, points = [[0,0],[1,2],[2,0],[2,2],[2,1]], k = 4

输出： 1

解释：

选择点 (0, 0) ，(2, 0) ，(2, 2) 和 (2, 1)。

示例 3：

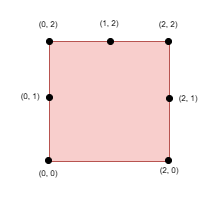
输入： side = 2, points = [[0,0],[0,1],[0,2],[1,2],[2,0],[2,2],[2,1]], k = 5

输出： 1

解释：

选择点 (0, 0) ，(0, 1) ，(0, 2) ，(1, 2) 和 (2, 2)。

提示：

  • 1 <= side <= 10^9
  • 4 <= points.length <= min(4 * side, 15 * 103)
  • points[i] == [xi, yi]
  • 输入产生方式如下：
    • points[i] 位于正方形的边界上。
    • 所有 points[i] 都 互不相同 。
  • 4 <= k <= min(25, points.length)

题解

没来得及做

全服第一解法

  • 将所有点映射到环上的参数值，并排序。
  • 复制一份点集并加上 4*side，用于处理环的循环特性。
  • 使用二分法在范围 [0, 2*side] 内搜索最大可能的最小距离。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
def solve(side, points, k):
    # 将正方形边界的点映射到环上的参数值
    def boundary_param(x, y, side):
        if x == 0:  # 点在左边
            return y
        elif y == side:  # 点在上边
            return side + x
        elif x == side:  # 点在右边
            return 2 * side + (side - y)
        else:  # 点在下边
            return 3 * side + (side - x)

    # 将每个点映射到环上的参数值，并排序
    p = []
    for x, y in points:
        p.append(boundary_param(x, y, side))
    p.sort()  # 对参数值排序
    n = len(p)
    # 复制一份并加上 4*side，用于处理环的循环特性
    e = p + [val + 4 * side for val in p]

    # 检查从某个起点开始，是否可以选择 k 个点，满足最小距离为 d
    def can_pick_start(i, d, next_idx):
        count = 1  # 已选点数
        cur = i  # 当前点的索引
        limit = e[i] + 4 * side - d  # 最大允许的环上位置
        while count < k:
            nxt = next_idx[cur]  # 下一个点的索引
            if nxt >= i + n:  # 超出范围，无法选择足够点
                return False
            if e[nxt] > limit:  # 下一个点超出最大允许位置
                return False
            cur = nxt  # 更新当前点
            count += 1  # 更新已选点数
        return True

    # 检查是否存在一种选择方式，使得最小距离为 d
    def feasible(d):
        # 预处理每个点的下一个点的索引
        next_idx = [0] * (2 * n)
        s = 0
        for j in range(2 * n):
            # 找到第一个满足 e[s] >= e[j] + d 的点
            while s < 2 * n and e[s] < e[j] + d:
                s += 1
            next_idx[j] = s  # 记录下一个点的索引
        # 检查每个起点是否满足条件
        for i in range(n):
            if can_pick_start(i, d, next_idx):
                return True
        return False

    # 二分法搜索最大可能的最小距离
    left, right = 0, 2 * side  # 初始搜索范围
    while left < right:
        mid = (left + right + 1) // 2  # 取中间值
        if feasible(mid):  # 如果 mid 可行，尝试更大的值
            left = mid
        else:  # 否则，尝试更小的值
            right = mid - 1
    return left  # 返回最大可能的最小距离

class Solution:
    def maxDistance(self, side: int, points: List[List[int]], k: int) -> int:
        return solve(side, points, k)
LeetCode
#周赛
LeetCode-第438场周赛
https://furthur509.github.io/2025/02/23/LeetCode-第438场周赛/
作者
Yang Mingxin
发布于
2025年2月23日
许可协议